In this activity, I tried to manipulate the histogram of a dark image to enhance the contrast. This allows the details in the dark regions of the image to appear.
Wait a second, what exactly is a histogram?
I mentioned the term previously but I haven't discussed it yet. My bad.
A histogram is a representation of the occurrences of data points. In image processing, we are concerned with the brightness histogram of an image. Each pixel in the image will have a specific brightness, and thus creating a histogram of the image will display the frequency of each level of brightness (from 0 to 255). In brightness histograms, we will not be dealing with the location of the points containing these levels of brightness. Since it displays the frequency of each value, it can also be viewed as a probability distribution. Hereafter, histogram and/or probability distribution function (PDF) will be used instead of brightness histogram for simplicity.
For the activity, we will be dealing with grayscale images. We expect that for a dark image, the histogram will be skewed towards the far left, near the zero value of intensity.
So before we proceed, here's a summary of the activity:
Figure 1. Flowchart
To be able to understand this, I'll give an example.
In this picture, (I can't remember who took this photo, I just found this somewhere in my astrophoto folders), the small amount of light makes it difficult to see a lot of details at the bottom part. Well, the CS basketball court would be the best place to set up a telescope because there are no lamps nearby (except those around NIP) and it's safe. So if you want to observe the night sky with a telescope, this is one of the nicest place in UP for observation. :D
In any case, at the lower part of the image, I'm there preparing the telescope. And there are bags nearby. But since it's dark, it's difficult to notice.
Figure 2. Image to be manipulated
Converting this to grayscale with Scilab:
Figure 3. Grayscale version of Figure 2
Here's the normalized histogram/PDF of Figure 3:
Figure 4. Normalized histogram of Figure 3. The frequencies of the intensities are divided by the total number of pixels in the image to normalize the histogram.
As you can see, the frequencies are high only at the 0-50 intensity levels. The image really is dark. So to enhance it, we introduce the concept of cumulative distribution function (CDF). Simply put, it is obtained by adding the normalized frequency at each value (in this case the intensity/ brightness level). The CDF of Figure 4 is:
Figure 5. Cumulative distribution function of the histogram in Figure 4.
We need another CDF, which is what we want to achieve for the original image. First, we use a linear CDF as our target CDF. For all brightness level in the image, there exists a CDF value in Figure 5. We then find this CDF value on the second CDF and determine the corresponding brightness level.
Figure 6. Obtaining the new pixel value using the original CDF (left) and the desired CDF (right)
If it's hard to process what I said in the previous paragraph, maybe Figure 6 can help. This shows that all pixels in the grayscale image with 30 as the brightness level will now have an intensity of 210. The final image, after applying this transformation is:
Figure 7. Enhanced image using a linear CDF
Works like magic. Haha. There, you can see me clearly and also my friend's bag. In addition, the letters from the word "NATIONAL" became more visible. You can also see the three-point "line" and the difference in the type/color of paint between the parts of the basketball court.
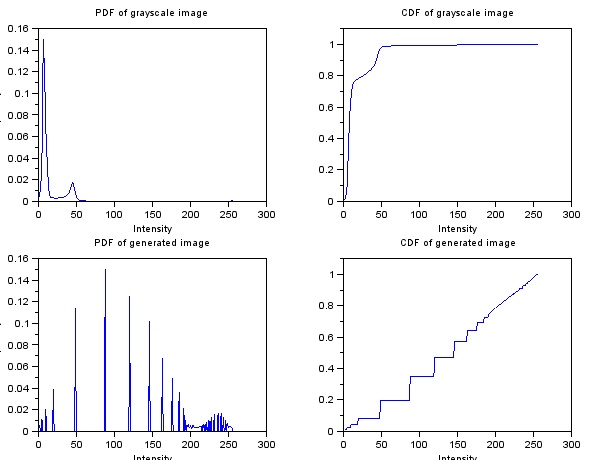
Here are the PDF's and CDF's of the grayscale and generated image:
Figure 8. Histogram and CDF of the image before (top) and after (bottom)
The spread of the histogram, after linearization of the CDF, became wider across 0 to 255. Also, the plot at the lower right of Figure 8 shows the CDF of the new image, which shows that indeed the CDF became linearized.
I also tried using a Gaussian distribution with varying standard deviation to manipulate the image. And here are the generated image, followed by the PDF's and CDF's.
Figure 9. Enhanced grayscale image. Standard deviation of 20 brightness levels were used for the Gaussian distribution, centered at 255/2.
Figure 10. Histogram and CDF of the image before (top) and after (bottom)
Figure 11. Enhanced grayscale image. Standard deviation of 40 brightness levels were used for the Gaussian distribution, centered at 255/2.
Figure 12. Histogram and CDF of the image before (top) and after (bottom)
You can see that the transitions between different objects in Figure 11 are more pronounced. This is because the brightness levels near zero and 255 have more frequency, as seen in the lower left plot in Figure 12, compared to that in Figure 10. Since the brightness levels peak at the mean brightness level and the distribution is narrow (standard deviation of 20 levels). Going back to the original concept, what we wanted was a histogram with values scattered from 0 to 255 right? We weren't able to see details in Figure 3 because its histogram is skewed towards zero. Even though the image became brighter in Figure 9, the distinctions between adjacent objects are not clear. With Figure 11, we obtained a relatively better image.
Let's use another image!
Figure 13. New image to be manipulated.
I took this image last February at the PAGASA Observatory in UP Diliman. The kids in the photo were having a field trip, waiting for the sun to set. During that night, they were able to spot Jupiter using the 45cm telescope of PAGASA. And here is its grayscaled version:
Figure 14. Grayscale version of Figure 13
Applying the same linear CDF, I obtained this image, followed by the original and resulting histograms and CDF's:
Figure 15. Resulting image after using a linear CDF
Figure 14. Histogram and CDF of the image before (top) and after (bottom)
Surprisingly, the enhanced image showed the shadow of the kids produced by the setting sun. The details of the plants, bushes, and trees appeared, as well as those on the building at the left (National Institute of Molecular Biology Building) and at the right (Kamia Residence Hall, I guess?).
It really worked like magic haha.
I also tried reproducing Figure 14 with GIMP using the Curves function under the Color Menu:
Figure 15. Enhancing the image in Figure 14 using GIMP.
Figure 16. Resulting image from GIMP
Figure 17. Histogram of Figure 16
With GIMP, I was able to make the histogram distributed over all the brightness levels, which is somehow similar to the lower left plot in Figure 14.
Out of 10, I would give myself a grade of 10 since I performed all the tasks well. Without Alix, I could not have done this activity. haha. At first, I manipulated the image pixel by pixel with the use of loop within a loop. It took an eternity to finish running, and produced nothing. Then she approached me and gave an overview of how she performed the manipulation. She taught me how to use the find() function properly. What I had in mind at first was to look for the pixel coordinates with certain brightness levels and collect their indices. She told me that I can just call the indices directly instead of storing them by appending the find() function to the matrix:
imgray2(find(imgray1==0)) = 255;This line, for example, uses two matrices of equal dimensions. The first one, imgray1, contains the brightness levels of all the pixels from an image. With find(imgray1==0), the indices of all black pixels will be collected. putting that inside imgray2() calls these indices from the second matrix, and then we assign them with a value of 255. Creating an image from imgray2, we will see that it will be the same as the original image, only that the black pixels from the original image will become white.
So there you have it. manipulation of images using histograms. Hope you enjoyed it. :D
References:
[1]. Soriano, M. Applied Physics 186 activity manual - enhancement by histogram manipulation.


















No comments :
Post a Comment